MAT100 Multivariable Calculus

Vector valued functions of one variable

A vector valued function of one variable is a function

\[\begin{align*} \mathbf r:D&\to\mathbb R^n\\ t &\mapsto \mathbf r(t)=(r_1(t),r_2(t),\ldots, r_n(t) ) \end{align*}\]

Where \(D\subset \mathbb R\).

Typical application:

• \(t\) represents time,
• \(\mathbf r(t)\) the position of an object at time \(t\).

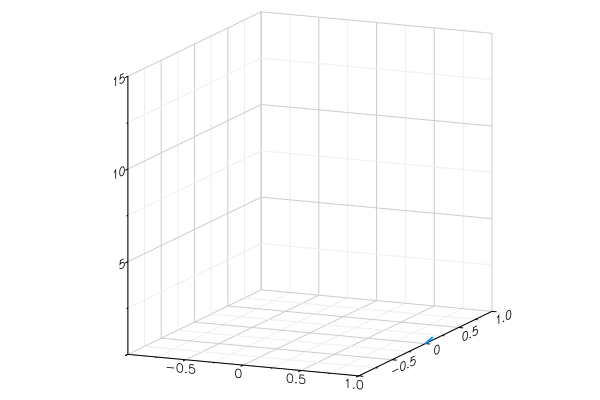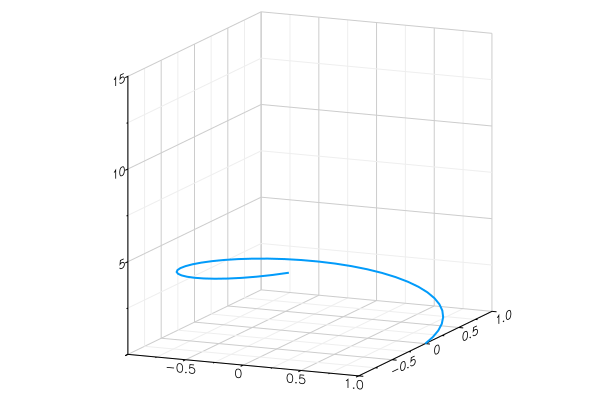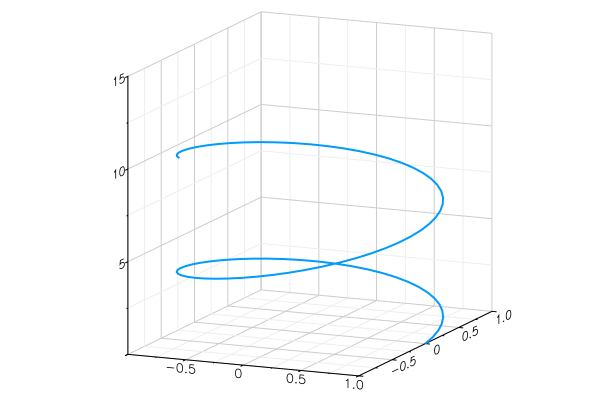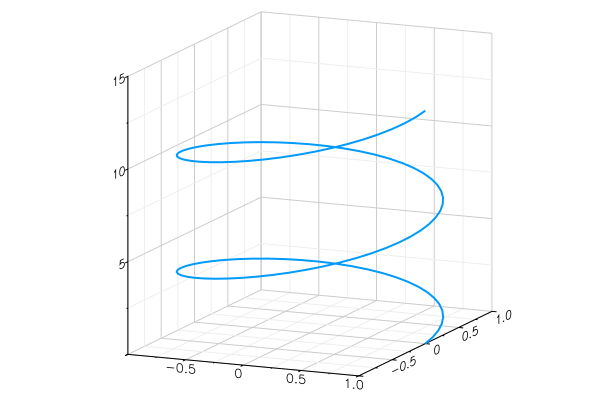
We can visualise such functions using parametric plots : plot the point \(\mathbf r(t)\) for each value of \(t\).

Examples

\[\mathbf r:[0,1]\to \mathbb R^2, \quad \mathbf r(t)=(1+t,t)=(1,0)+t(1,1)\]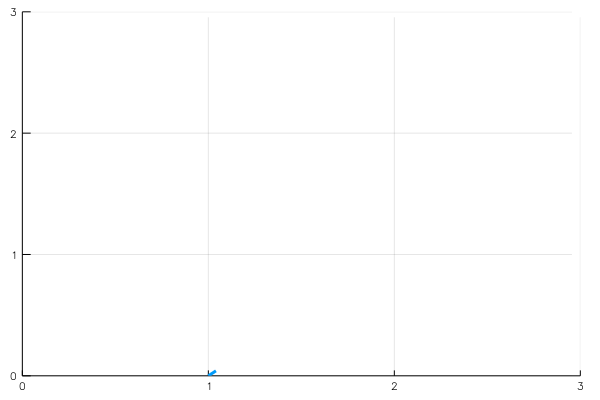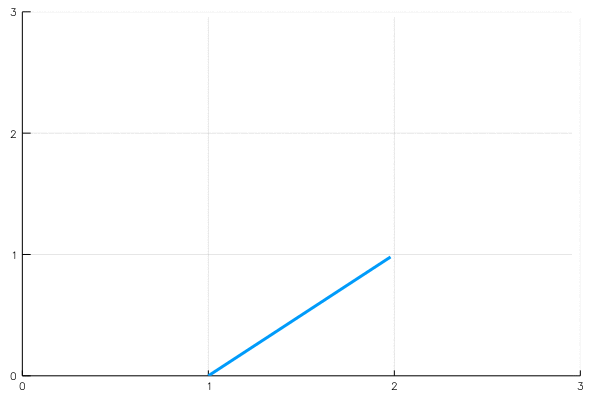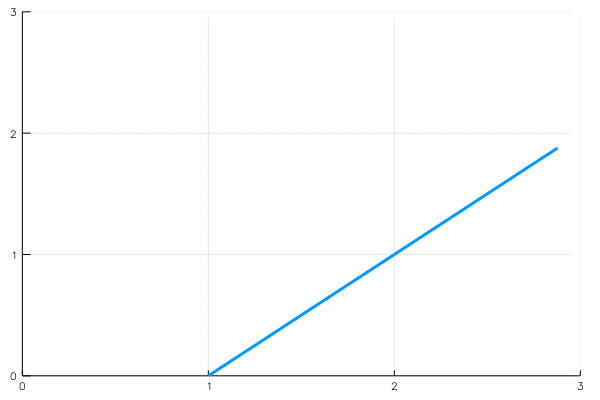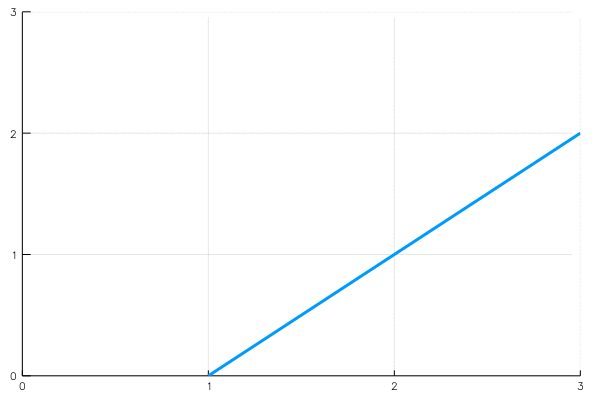

---

\[c:[0,2\pi]\to \mathbf R^2,\quad \mathbf c(t)=(\cos(t),\sin(t))\]

---

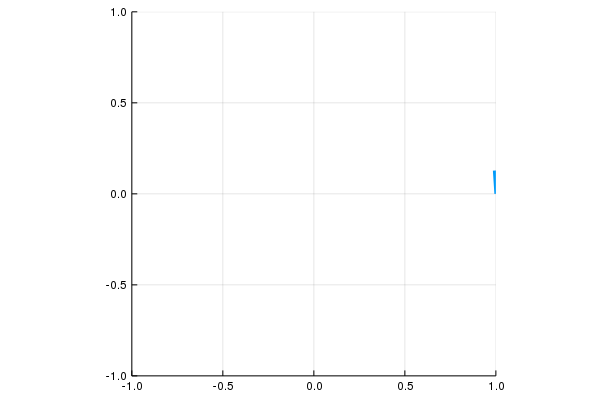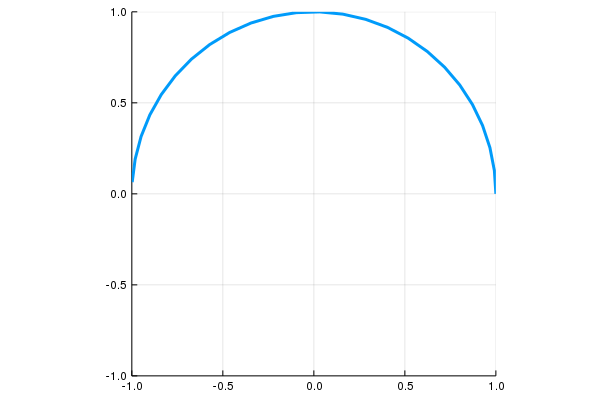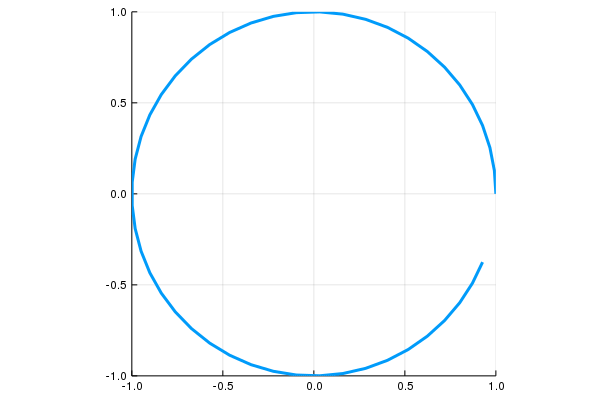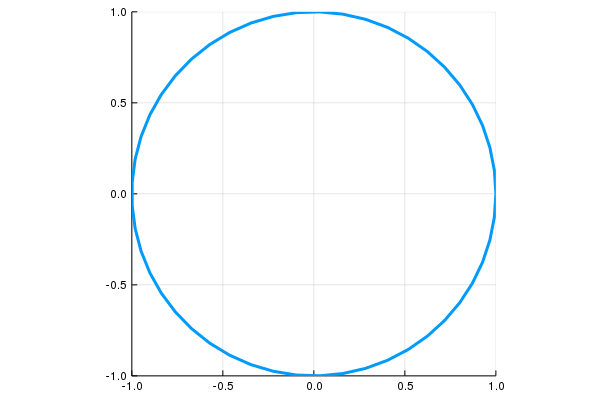
\[c:[0,1]\to \mathbf R^2,\quad \mathbf c(t)=(\cos(2\pi t),\sin(2\pi t))\]

---

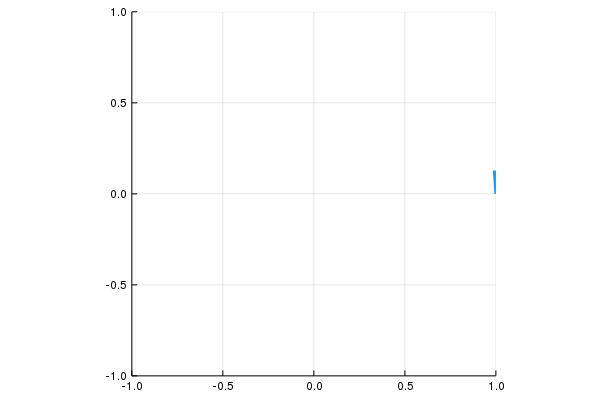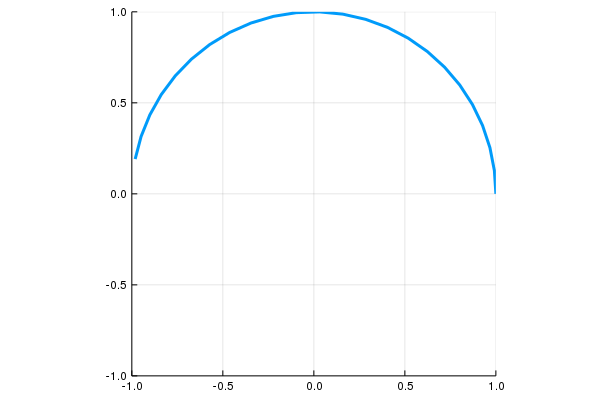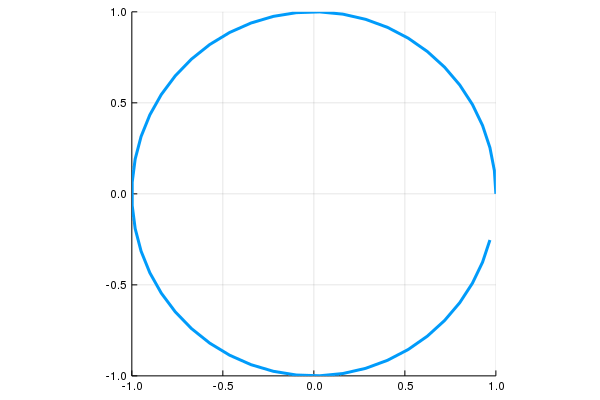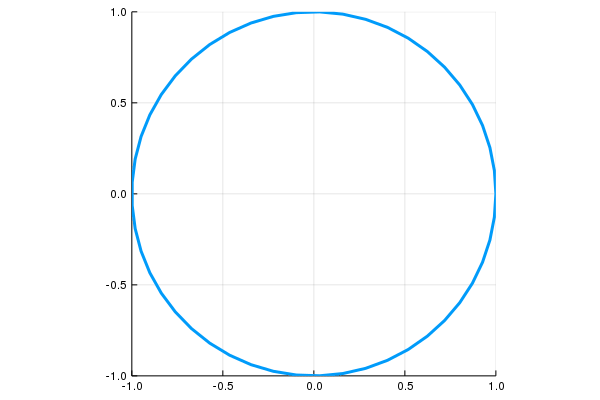
\[\mathbf r:[0,4\pi]\to\mathbb R^3,\quad \mathbf r(t)=(\cos t,\sin t,t )\]