Research

I’m interested in geometric variational problems and flows, differential geometry, and global analysis.

Currently my research focuses on geometric Sobolev gradient flows. For example, the well-known curve-shortening flow follows an \(L^2(ds)\) gradient of the length of a curve, where \(ds\) is the arc-length measure. However, by a result of Michor and Mumford the Riemannian metric induced by \(L^2(ds)\) on the space of immersed curves is actually trivial. This suggests that one might discover some interesting behaviour by considering other gradients, such as those induced by Sobolev metrics. Below is an animation of the evolution of a closed curve under the \(H^1(ds)\) curve-shortening (see preprint, joint work with Glen and Valentina Wheeler).

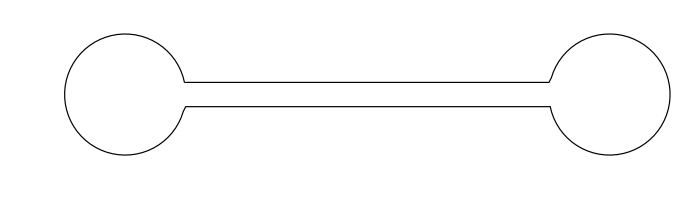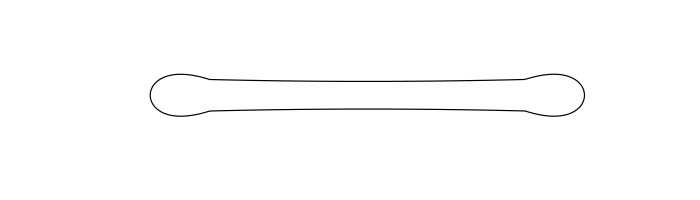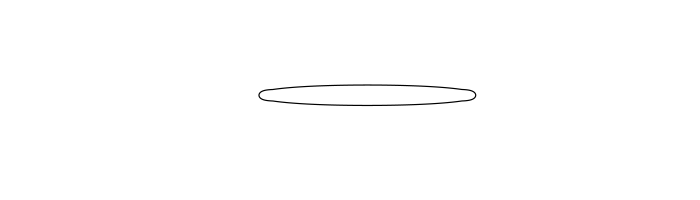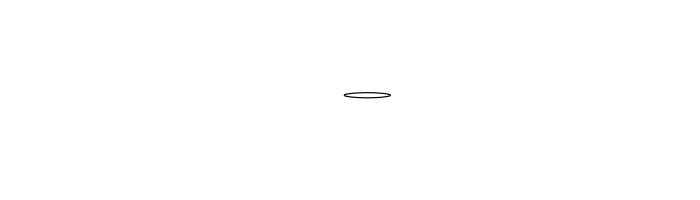
Preprints

S. Okabe, P. Schrader Convergence of Sobolev gradient trajectories to elastica, 2021

P. Schrader, G. Wheeler and V.-M. Wheeler, On the \(H^1(ds)\)- gradient flow for the length functional, 2021

Publications

P. Schrader, Morse theory for elastica. J. Geom. Mech., 8(2):235–256, 2016.

P. Schrader. Existence of variationally defined curves with higher order elliptic Lagrangians. Nonlinear Anal., 115:1–11, 2015.

P. Schrader and L. Noakes. Conditional extremals in complete Riemannian manifolds. Nonlinear Anal., 75(4):2177–2188, 2012.

Ph.D. thesis

Schrader, P. J. (2016). Global analysis of one-dimensional variational problems.